Кружковцам следует рассказать о том, что наиболее совершенным устройством автоматического управления является управляющая машина с ее главным узлом — вычислительным устройством. С помощью управляющей машины может осуществляться автоматическое управление целыми цехами и заводами. Применение управляющих машин создает условия для комплексной автоматизации производственных процессов.
Автоматизация процесса решения сложных математических задач имеет исключительно большое значение для технического прогресса народного хозяйства нашей страны. Системы, выполняющие подобные функции, называются автоматическими вычислительными системами. В настоящее время особенное распространение получили электронные вычислительные системы. Автоматические вычислительные системы подразделяются на аналоговые, или непрерывного действия; цифровые, или дискретного действия.
В своих беседах руководителю следует остановиться на обеих системах и более подробно рассмотреть структурную схему быстродействующей электронной вычислительной машины дискретного действия.
Аналоговая система основана на аналогии между математическими уравнениями, описывающими ее поведение, и уравнениями, характеризующими свойства некоторого физического объекта, подлежащего исследованию. Действия над математическими величинами заменяются действиями над физическими величинами, причем физические величины могут изменяться непрерывно и принимать любые значения, соответствующие значениям математических величин. Эти устройства, как правило, состоят из отдельных блоков, выполняющих те или иные математические действия.
Основными блоками являются следующие:
1) функциональные преобразователи (блоки для построения заданных математических функций);
- блоки суммирования переменных (выполнение операций сложения и вычитания);
- блоки умножения переменной величины на постоянный коэффициент;
- блоки умножения переменных;
- блоки деления переменных;
- блоки дифференцирования;
- блоки интегрирования.
Поскольку усвоение принципа работы большинства из вышеперечисленных блоков вызывает у школьников определенные трудности, им следует дать только общие представления о сущности выполняемых аналоговыми устройствами операций. Наиболее доступно для ребят рассмотреть отдельные функции и математические действия, которые могут выполняться потенциометрами.
Потенциометры служат для преобразования механической величины в электрическую, построения математических функций, выполнения операций умножения и деления и в соединении со следящей системой для преобразования электрической величины в механическую.
По принципу действия применяемые в аналоговых устройствах потенциометры ничем не отличаются от обычных проволочных переменных резисторов. На каркас из изоляционного материала намотана проволока высокого сопротивления, по которой скользит щетка. Питающее напряжение U подается на концы обмотки. Выходное напряжение U2 снимается между одним из концов обмотки и щеткой (через токосъемное кольцо). Зависимость выходного напряжения от угла поворота щетки определяется формой каркаса. Если каркас равномерный (такой потенциометр называют линейным; ширина его на всем протяжении одинакова), то выходное напряжение пропорционально входному напряжению и углу поворота:
U2 - Uxx,
где х — величина, характеризующая угол поворота оси потенциометра.
Из этого следует, что при неподвижном положении щетки линейный потенциометр может служить в качестве блока умножения на постоянный коэффициент, меньший единицы, так как х больше единицы быть не может.
Линейный потенциометр может также служить в качестве блока умножения двух переменных, одна из которых представлена механической величиной х, а другая — электрической величиной U. Произведение при этом получается в виде электрической величины U2,
В автоматических вычислительных системах часто бывают необходимы нелинейные функциональные потенциометры, позволяющие получать заданную функциональную зависимость между выходным напряжением потенциометра и углом поворота его оси. Нелинейную зависимость получают путем выполнения каркаса с неравномерной шириной или шунтирования отдельных участков потенциометра. Например, для получения квадратичной функции f(x)=x2 каркас должен иметь треугольную форму, для логарифмической функции f(x)=nx каркас должен быть гиперболическим, а для синусоидальной функции f(x)=smx — косинусоидальным.
Пользуясь кусочно-линейной аппроксимацией заданной функции, можно построить функциональный потенциометр с равномерным каркасом, отдельные участки которого шунтированы сопротивлениями. Здесь шунтирование равносильно уменьшению ширины каркаса.
Потенциометр является гибким устройством, что обусловливает его многообразное применение в аналоговых вычислительных системах, питаемых как постоянным, так и переменным напряжением.
На занятиях кружка может быть построено простейшее вычислительное устройство — мостовая схема умножения и деления, состоящая из четырех линейных потенциометров и чувствительною стрелочного измерительного прибора в качестве индикатора баланса моста.
Условием равновесия моста является соотношение:
R2R3 = R1R4.
Любое изменение R9 R2 или R3 вызывает изменение R4. Следовательно, вычислительное устройство позволяет выполнять следующую математическую операцию:
Y=2*3 Хх
Для проведения вычислений потенциометры R1, R2 и R3 следует снабдить шкалами. Потенциометр R4 служит для балансировки моста и отсчета результата (рис. 54)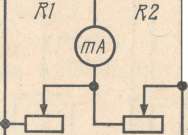
Рис. 54
В цифровых вычислительных системах величины, над которыми производятся математические действия, выражаются в виде чисел в цифровой форме. Все математические задачи в таких системах сводятся к последовательному выполнению четырех арифметических действий. В отличие от аналоговых систем, где точность решения ограничена точностью элементов, в цифровых системах точность зависит лишь от количества знаков (разрядов) в изображении чисел и может быть чрезвычайно высокой.
Для быстрого решения задач требуется полная автоматизация всего процесса решения и большая скорость выполнения операций. Автоматизация решения достигается в них с помощью программного управления всем процессом вычислений. При этом машина обладает возможностью хранения (запоминания) весьма большого числа исходных и промежуточных данных. Машина автоматически выбирает направление дальнейших вычислений в зависимости от промежуточных результатов. Быстродействие машины достигается за счет применения электронных элементов.
Структура автоматической цифровой вычислительной машины основывается в общих чертах на тех действиях, которые производит человек при выполнении расчетов с помощью карандаша и бумаги. Расчетчик, пользуясь заданным порядком расчета, выполняет арифметические операции и записывает (запоминает) исходные, промежуточные и итоговые данные.
Соответственно цифровая машина состоит из следующих основных устройств:
- устройство ввода данных;
- арифметическое устройство;
- запоминающее устройство;
- устройство управления;
- устройство вывода результатов.
Структурная схема цифровой машины показана на рис. 55.
Устройство ввода данных служит для введения в машину исходных чисел и программы вычислений. Программа представляет собой последовательность команд. Команда содержит указания, где находятся числа и какую операцию над ними следует произвести. Программа записывается на перфокартах, перфоленте или магнитной ленте. Команда и числа представляются в виде кодов. Программа составляется заранее и вводится в машину перед решением задачи. При введении программы числа и команды фиксируются в ячейках запоминающего устройства. После того как программа введена в запоминающее устройство, все решение производится автоматически.
Арифметическое устройство выполняет основные операции над числами: сложение, вычитание, умножение и деление. Поэтому арифметические устройства содержат сумматоры, блоки умножения .и блоки деления. Арифметические операции могут производиться последовательно и параллельно Соответственно машины называются машинами последовательного или параллельного действия. В машине последовательного действия операции выполняются разряд за разрядом, как при ручном счете. Такие машины являются сравнительно простыми, но относительно медленно действующими. В машинах параллельного действия операции выполняются над всеми разрядами одновременно, что обеспечивает более высокую скорость вычислений, но требует большого количества оборудования.
В арифметическое устройство поступают числа из запоминающего устройства. Над числами производится действие в соответствии с кодом операции. Число, являющееся результатом операции, снова отправляется в запоминающее устройство.
В зависимости от признака промежуточного результата (например, от того, положительный или отрицательный знак имеет полученное число) из арифметического устройства в устройство управления передается сигнал, изменяющий соответствующим образом последовательность операций.
Запоминающее устройство хранит введенные в него исходные данные и команды, а также промежуточные результаты. Цифровые машины обычно содержат внеш ние и внутренние запоминающие устройства.
Внешние запоминающие устройства обладают боль шой емкостью, но малым быстродействием. Они содержат большое число данных, которые непосредственно не участвуют в операциях, а служат резервом для внутрсн него запоминающего устройства. Внешнее запоминающее устройство выполняется большей частью на магнитных лентах.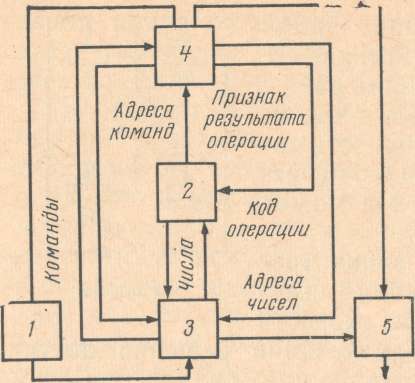
Внутреннее (оперативное) запоминающее устройство имеет относительно малую емкость и высокое быстродействие. Оно служит для запоминания промежуточных результатов и других данных, необходимых для выполнения операций. Оперативное запоминающее устройство выполняется обычно на магнитных сердечниках.
Устройство управления обеспечивает автоматическое выполнение программы, введенной в машину. Оно содержит генератор, выдающий управляющие импульсы, которые определяют ход работы машины. Устройство управления посылает в запоминающее устройство адреса очередных команд (номера ячеек, где хранятся команды). Команды выбираются из запоминающего устройства и направляются в устройство управления, где они расшифровываются. В соответствии с адресом, указанным в команде, происходит передача числа из запоминающего устройства в арифметическое устройство, и соответствующий код операций настраивает арифметическое устройство на выполнение необходимой операции. Полученное число направляется по адресу результата в запоминающее устройство. В соответствии с признаком результата операции управляющее устройство может изменять ход дальнейших вычислений. Устройство управления посылает также необходимые сигналы в устройство ввода и вывода данных.
Устройство вывода результата служит для получения окончательных результатов вычислений. Обычно эти результаты получаются в машине на перфокартах, перфолентах или магнитных лентах, а затем автоматически перепечатываются в виде цифровых таблиц.
В вычислительных устройствах большей частью используется двоичная система счисления, так как она легко реализуется с помощью двухпозиционных элементов: электронных, магнитных и полупроводниковых триггеров. В двоичной системе любое целое число представляется как сумма величин 2°,2 22, 23 и т. д., каждое из которых может быть взято лишь 0 или 1 раз. Например: 26= 1.24+1.23+0.22+1.21 + 0.2°. Запись числа в двоичной системе будет 11010 (считая справа налево), т. е. в данном числе отсутствует 2°, имеется 21, отсутствует 22 и имеются 23и 24.
Для сравнения следует рассмотреть представления числа в десятичной система. Например, 26=2.101-^б. 10°, т. е. основанием является 10.
Далее членам кружка сообщают, что арифметические действия над двоичными числами производятся так же, как и над десятичными. Чтобы убедиться в этом, на доске производят основные операции над числами в обеих системах.
|
Таблица 44 Основные операции, производимые над числами в обеих системах
|
|||||||||||||||||||||||||||||||
