Энергетический спектр. Кристалл может состоять из одинаковых атомов (атомарный кристалл) либо из атомов разных сортов. Как те, так и другие могут быть изоляторами, полупроводниками и металлами. Для простоты мы будем говорить только об атомарных кристаллах. Все основные выводы годятся и для кристаллов, состоящих из разных атомов.
Каждый кристалл содержит огромное число электронов. Так, например, кристалл германия, одного из типичных полупроводников, содержит примерно 1,3 • 1024 электронов в 1 см3. Тем не менее далеко не каждый кристалл является проводником. Оказывается, что электрические свойства кристалла зависят прежде всего от того, какими значениями энергии могут обладать его электроны. Совокупность этих значений называется энергетическим спектром электронов. Последний определяется характером сил, действующих на электрон.
Спектр свободного электрона. Свободный электрон (т. е. электрон, на который не действуют никакие силы) обладает кинетической энергией:
|
mv2 |
где т— масса, v— скорость электрона. Энергия свободного электрона может принимать любые значения е ^ 0 (при е = 0 электрон покоится). Энергетический спектр такого электрона называют непрерывным (сплошным).
Спектр электрона в атоме (атомный спектр). Известно, что энергия электрона в атоме может принимать только ряд вполне определенных значений, называемых уровнями энергии. Такой спектр называется дискретным. Его удобно представить в виде лестницы горизонтальных линий. Расстояние между двумя какими- либо уровнями (линиями) в некотором масштабе представляет собой разность соответствующих значений энергии (рис. 5.1, а).
Спектр электрона в кристалле (спектр кристалла). На каждый электрон в кристалле действует электрическая сила, обусловленная притяжением со стороны ядер и отталкиванием со стороны прочих электронов. Поскольку атомы кристалла расположены в пространстве периодически, эта сила также является периодической в пространстве. Говорят, что электрон в кристалле находится в периодическом электрическом поле.
Спектр электрона в периодическом поле изображен на рисунке 5.1, б. Заштрихованные интервалы энергии — области, внутри которых энергия электрона может принимать любое значение. Это так называемые зоны разрешенных значений энергии — разрешенные зоны. Последние отделены друг от друга незаштрихованными интервалами. Электрон не может обладать каким-либо значением энергии, лежащим в незаштрихованной области. Это зоны запрещенных значений энергии, или запрещенные зоны (ниже разрешенная зона именуется просто зоной). Энергетический интервал между нижней и верхней границами рассматриваемой зоны (между «дном» и «потолком» зоны) называется шириной зоны. Интервал между потолком данной зоны и дном соседней, более высокой зоны называется шириной запрещенной зоны.
Каждый электрон кристалла находится в определенной зоне, т. е. обладает энергией, значение которой лежит внутри одной из разрешенных зон.
Сравнение атомного и кристаллического спектров. Полезно сопоставить спектры (рис. 5.1, а и б). Предположим, что кристалл состоит из атомов, расположенных друг от друга на столь большом расстоянии, что взаимодействием между атомами можно пренебречь. Такой кристалл является просто совокупностью периодически расположенных изолированных атомов, а его спектр совпадает с атомным (рис. 5.1, а). Этот спектр можно представить как спектр рисунка 5.1, б, в котором зоны сузились и превратились в уровни. Таким образом, если взаимодействие между атомами ослабевает, то зоны сужаются, и наоборот, при увеличении взаимодействия между атомами уровни расплываются в зоны. Чем сильнее взаимодействие, тем шире зоны.
В системе невзаимодействующих атомов каждый электрон постоянно находится только в пределах «своего» атома. При наличии взаимодействия электрон может переходить от одного атома к другому. Можно сказать, что рисунок 5.1, а представляет спектр электрона, находящегося в определенном атоме, рисунок 5.1, б — спектр электрона, который может перемещаться по кристаллу.
Из сравнения рисунков 5.1, а и б можно сделать ряд важных выводов. Прежде всего указать, какому атомному уровню соответствует данная зона. Далее, известно, что чем выше уровень энергии электрона в атоме, тем дальше в среднем от ядра находится электрон. В силу соответствия между уровнями атома и зонами кристалла то же самое можно сказать и относительно электронов в зонах: чем выше по энергии расположена зона, тем в среднем дальше от ядер находятся соответствующие электроны и следовательно, тем сильнее они взаимодействуют с окружающими атомами.
Состояние электрона в кристалле. Свободный электрон, электрон в атоме или в кристалле может находиться в различных состояниях.
Состояние определяется значением ряда физических величин, характеризующих движение электрона. Так, состояние свободного
|
97 |
электрона определяется вектором скорости v,т. е. совокупностью трех чисел — трех проекций скорости: vx>vи у . Электроны с
-v -*■ У
разными скоростями v1и v2находятся в разных состояниях, но
они могут обладать одинаковой энергией, если (иг)2 = (v2)2(скорости отличаются только по направлению).
Рассмотрим теперь состояние электрона в атоме. Из школьного курса химии известно, что траектория электрона в атоме заполняет некоторую область пространства вокруг ядра, называемую электронным облаком. Состояние электрона определяется формой этого облака. Если форма облака одного электрона отличается от формы другого, то состояния этих электронов различны. Так же как и для свободного электрона, среди различных состояний имеются такие, энергии которых одинаковы, т. е. разные состояния могут соответствовать одному и тому же уровню энергии.
Состояния электрона в кристалле отличаются прежде всего номером зоны. Внутри данной зоны состояния также могут быть различными. Каждое состояние внутри зоны, как и состояние свободного электрона, характеризуется значением вектора скорости. Таким образом, электрон, находящийся в определенном состоянии, движется по кристаллу.
Число электронов в данном состоянии. Сколько электронов может одновременно находиться в данном состоянии? В классической механике это число ничем не ограничено. Например, любое число свободных электронов может одновременно иметь одну и ту же скорость.
В квантовой механике положение радикально меняется. Вспомним, что говорится в школьном курсе химии об электронах в атоме: одновременно не более двух электронов может иметь облако одинаковой формы, т. е. находиться в одинаковом состоянии. Оказывается, это положение является частным проявлением общего правила: в данном состоянии может находиться не более двух электронов. Это утверждение в равной мере относится к свободным электронам, к электронам в атоме или кристалле. Оно носит название принципа Паули. Принцип Паули играет в современной физике огромную роль. Состояние называется заполненным, если в нем находится два электрона.
Число состояний. Электронное облако атома состоит из ряда оболочек. Существует максимальное количество электронов, которые могут находиться в данной оболочке. Следовательно, число состояний в оболочке конечно, так как в силу принципа Паули в одном состоянии не может быть больше двух электронов. Число состояний можно получить, разделив максимальное количество электронов оболочки на два. Так, в первой, самой близкой к ядру оболочке может быть не более двух электронов. Значит, в этой оболочке всего одно состояние. Следующая оболочка может содержать не более "восьми электронов, в ней—четыре состояния. В третьей — также четыре состояния, затем девять и т. д.
Число состояний в зоне также конечно. Замечательно, что оно одинаково для различных зон и равно числу атомов кристалла N. Можно сказать, что в зоне на каждый атом приходится одно состояние.
Подведем итог. Спектр электрона в кристалле представляет собой совокупность разрешенных зон, разделенных запрещенными промежутками. В любой зоне число состояний равно N. В данном состоянии может находиться не более двух электронов. В каждом состоянии электрон обладает некоторой скоростью.
Пустые, заполненные и частично заполненные зоны. Зона называется пустой, если в состояниях этой зоны нет ни одного электрона, и полностью заполненной, если в каждом ее состоянии находится по два электрона. Во всех других случаях говорят, что зона заполнена частично.
Перенумеруем все состояния зоны, обозначив индексом ано-
мер состояния. Электрон в состоянии аобладает скоростью иа,
Движущийся электрон создает некоторый ток, плотность этого то- -> —►
ка обозначим ja. Полная плотность тока /, создаваемая всеми электронами данной зоны, равна векторной сумме плотностей токов всех имеющихся в зоне электронов.
-*■
Если электронов в зоне нет, то j= 0. Если зона заполнена целиком, то и в этом случае j= 0. Это связано с симметрией кристалла, т. е. с периодическим расположением его атомов в пространстве. Равенство нулю плотности тока заполненной зоны можно записать следующим образом:
22 • U=0. (1)
а
В левой части равенства (1) суммирование производится по всем состояниям зоны. В каждом состоянии находится два электрона.
Важно, что равенство (1) верно и в том случае, если к кристаллу приложено электрическое поле Е.Так как при £=^0в каждом состоянии заполненной зоны по-прежнему находится два электрона, сумма (1) при включении поля измениться не может.
Иное дело зона, заполненная частично. При Е= 0 в такой зоне / = 0 просто в силу полной хаотичности теплового движения электронов. При Е Ф 0 на каждый электрон действует сила F= = —еЕ (е—абсолютная величина заряда электрона). Так как в зоне имеются свободные состояния, под действием силы Fпроисхо-; дит перераспределение электронов по состояниям и возникает отличная от нуля плотность тока /.
I1з изложенного выше следует очень важный вывод: кристалл мо- >м г быть проводником только при наличии частично заполненной ВОНЫ.
1 и пр. о и лиг электронов по зонам при абсолютном нуле. Ди-
II И Mj ............ 11\с.. ||. р.рпстплл состоит из атомовс атом
ным номером Z.Следователь он имеет ZNэлектронов. При абсолютом нуле (/ О К) любая система частиц находится в состоянии с наименьшей энергией. Как следует разместить ZNэлектронов по зонам, чтобы кристалл в целом обладал наименьшей nieniней?
Начнем размещать электроны в состояния самой низшей (первой) юны. Когда она окажется заполненной, будем заполнять 4 иною (вторую), затем третью и так далее, пока не разместим *н«* «лек фоны. Поскольку для заполнения каждой зоны требуется
1
Л\ I к'ктронов, то при четном Zбудет заполнено-^- первых зон, а
2
|нт зоны, начиная с зоны номер —+ 1, окажутся свободными. I я 2 2-1
Гг л и / нечетно, то будут полностью заполнены —— первых Z+1
i4.ii, нщ,! с номером - окажется заполненной частично, а все
и» т.н.мыс останутся пустыми. Таким образом, возможны две со- |и| но различные ситуации: 1) В кристалле существуют зоны пикт: полностью заполненные и совершенно пустые. Такой *|ни 1й ы пе может проводить электрический ток и является диэ- Агкфмком. 2) Среди зон кристалла существует одна, заполненная нано юниц) В этом случае кристалл оказывается проводником. Mim> м<inГ».2 иллюстрирует эти выводы (заполненные состояния
заштрихованы двойной штриховкой, свободные—одинарной): а, б соответствуют диэлектрику, в — проводнику.
Наивысшая заполненная при Т = О °К зона диэлектрика называется валентной (и-зона). Происхождение названия понятно: электроны этой зоны соответствуют электронам внешних оболочек атома, т. е. валентным электронам. Наинизшая из пустых при Т = О РК зон называется зоной проводимости (озона). Электроны, находящиеся вой озонах, называются соответственно валентными электронами и электронами проводимости.
Полупроводники. Рассмотрим диэлектрик при отличных от абсолютного нуля температурах. При Т Ф О °К ионы кристалла совершают хаотическое тепловое движение около положений равновесия. В результате взаимодействия с колеблющимися ионами (или другими электронами) электрон у-зоны может получить достаточную энергию и перейти в одно из состояний с-зоны. Одно состояние в с-зоне окажется занятым. В с-зоне возникнет'незанятое состояние — «дырка». Электрону, находящемуся у потолка с-зоны, требуется для такого перехода наименьшая энергия. Она равна ширине запрещенной зоны е^, отделяющей озону от с-зоны. В среднем при Т Ф О °К имеется некоторое количество электронов в озоне и дырок в озоне.
Наличие небольшого количества дырок в озоне и электронов в озоне создает условия для возникновения тока в диэлектрике при приложении электрического поля.
Сопротивление диэлектрика оказывается тем меньше, чем больше электронов переброшено из озоны в озону. При заданной температуре число переброшенных электронов, а следовательно, и сопротивление зависит от быстро увеличиваясь с уменьшением
Если энергия гк велика, сопротивление оказывается настолько большим, что возникающие токи не поддаются измерению: диэлектрик практически остается изолятором и при Т Ф О °К. Если же энергия невелика, то сопротивление может оказаться относительно небольшим. Такие диэлектрики получили название полупроводников.
Таким образом, полупроводник — это диэлектрик с относительно узкой запрещенной зоной, отделяющей верхнюю заполненную при Т = О °К зону от нижней незаполненной.
Различие между диэлектриком и полупроводником проиллюстрировано на рисунке 5.2: а—соответствует собственно диэлектрику, б— полупроводнику, в— проводнику.
Из сказанного следует, что различие между диэлектриками и полупроводниками количественное. Граница между ними не является четкой. Полупроводник — это кристалл, являющийся при Т = О °К диэлектриком, но имеющий относительно узкую запрещенную зону. Принято считать, что сопротивление полупроводников при комнатной температуре лежит в интервале от 10~[1] до 104 ом-м. Хорошо проводящий металл обладает сопротивлением порядка 10~8 ом-м, диэлектрик— 1010 ом-м.
Рождение пары и рекомбинация. Энергия электронов с-зоны выше, чем а-зоны. Поэтому они в среднем находятся дальше от ядер. Говорят, что электроны с-зоны слабее связаны с ядрами, такие электроны обычно называют свободными. При Т = О °К свободных электронов нет, озона пуста. С повышением температуры количество свободных электронов возрастает.
При Т — О °К озона полностью заполнена электронами. Ее можно также считать пустой в том смысле, что в ней нет ни одной дырки. С ростом температуры в о-зоне появляются дырки. По аналогии, эти дырки также называют свободными.
При Т Ф О °К в полупроводнике электроны непрерывно переходят из озоны в озону, происходит генерация пар электрон — дырка. Имеет место и обратный процесс — возвращение электронов в озону. Это— процесс рекомбинации пар. Генерация происходит тем интенсивней, чем выше температура. Чем больше число свободных электронов и дырок, тем больше вероятность их встречи и тем выше интенсивность рекомбинации. При каждой данной температуре генерация и рекомбинация находятся в динамическом равновесии друг с другом и средние концентрации свободных электронов (п) и дырок (р) постоянны. Если температура нозрас 1«1 с*!, генерация усиливается, и п и р начинают увеличиваться Это продолжается до тех пор, пока возросшая интенсивность рекомбинации не уравновесит генерацию. Таким образом, пир возрастают с повышением температуры.
Ток, создаваемый электронами валентной зоны. Чтобы вычислить плотность тока /, создаваемую электронами некоторой зоны, надо знать распределение электронов по состояниям. Электронов
и валентной зоне много, и для вычисления плотности тока / потребовалось бы суммировать огромное количество токов отдельных электронов. Оказывается, что это можно сделать гораздо проще.
Ток, создаваемый электронами полностью заполненной зоны, равен нулю. Пусть в сьзоне при температуре, отличной от абсолютного нуля, не хватает одного электрона, скажем, электрона в состоянии с а — 1. Тогда полная плотность тока этой зоны уже не равна нулю. Нетрудно сообразить, чему она равна. Предположим, что в незаполненное состояние возвращается электрон. Тогда к
плотности тока / у-зоны без одного электрона добавляется плот-
ность тока ]\ возвратившегося электрона и плотность тока а-зоны
становится равной j+ jvНо теперь н-зона целиком заполнена, и суммарная плотность тока всех ее электронов должна равняться
нулю / -4 /А = 0. Отсюда:
7 = —Jv (2)
т. е. плотность тока в зоне, в которой незаполнено одно состояние, равна плотности тока отсутствующего электрона с обратным знаком. Вместо того чтобы суммировать огромное количество токов электронов, находящихся в a-зоне, достаточно знать ток одного- единственного ушедшего электрона.
Вообразим теперь, что электронов в ц-зоне вообще нет, но в состоянии 1 имеется частица с зарядом +е, где е — абсолютная величина заряда электрона. Такой заряд как раз и будет создавать плотность тока — Д. Таким образом, ток зоны, в которой нет одного электрона, равен току одной дырки. Понятие «дырка» теперь уже не просто термин, означающий незанятое состояние. Дырку следует рассматривать как некоторую частицу с положительным зарядом +е, находящуюся в том состоянии, в котором нет электрона, т. е. имеющую ту же скорость, которой обладал бы электрон в этом состоянии.
Этот вывод можно обобщить на зону с любым количеством пустых мест: если в зоне не хватает двух электронов, плотность тока равна сумме плотностей токов двух дырок; вообще, ток произвольным образом заполненной зоны можно вычислить, просуммировав либо токи всех имеющихся электронов, либо всех дырок. Ясно, что если электронов мало, проще подсчитывать электроны, а если зона заполнена почти полностью, — дырки.
В действительности, преимущество рассмотрения дырок, а не электронов, в случае почти заполненной зоны, связано не только и даже не столько с тем, что электронов много, а дырок мало. Понятие «дырка» оказывается гораздо более глубоким: почти заполненная зона во всех отношениях ведет себя так, словно переносчиками заряда в этой зоне являются положительные частицы. Именно это и имеют в виду, когда говорят, что проводимость зоны имеет дырочный характер.
Удельная проводимость полупроводника. У величин, относящихся к свободным электронам, будем ставить индекс п, а к свободным дыркам — индекс р.
В курсе физики 9-го класса показано, что молекулярно-кинетическая теория приводит к формуле, связывающей плотность тока
электронов /п и электрическое поле Е внутри проводника:
In= К(3)
где — удельная проводимость электронов, связана с концентрацией п и коэффициентом трения knсоотношением kn= В случае полупроводника обычно вводят так называемую подвижность электронов рп, связанну зуя pnдля получим:
К = «Ч* »
индекс gот английского слова —зазор,разрыв.
Аналогично для плотности тока дырок jpможно написать:
jP= \Е, (5)
где проводимость дырок 'Кр связана с подвижностью дырок формулой:
К = Wp- (6)
Полнаяплотность тока /равна сумме jn и jp: / = jn + jp.Используявыписанные вышеформулы для полнойпроводимости полу
проводника А,, определяемой соотношением / = ХЕУ нетрудно получить:
X = Ъп + Ьр= ещп + вр[1р. (7)
Зонная схема для полупроводника. Графически и- и с-зоны полупроводника и распределение свободных носителей в зонах изображаются следующим образом (рис. 5.3). Горизонтальные линии гс и evизображают соответственно дно озоны и потолок озоны. Расстояние между этими линиями равно ширине запрещенной зоны eg.Область выше ес соответствует озоне, область ниже ev— озоне. Кружки со знаком «минус» — свободные электроны, со знаком «плюс» — свободные дырки. На рисунке 5.3 имеются два свободных электрона и две свободные дырки.
Схемы валентных связей. Валентная зона — наивысшая из зон, заполненных при абсолютном нуле. Ее электроны соответствуют электронам внешних оболочек атома. Эти электроны сильнее других взаимодействуют с соседними атомами в кристалле. Благодаря этому взаимодействию возникают силы сцепления — валентные связи, а совокупность атомов превращается в единое целое— кристалл. Таким образом, электроны ц-зоны образуют валентные связи н кристалле. На рисунке 5.4 воспроизведена схема пространственного распределения валентных связей в кремнии (Si), приведенная и учебнике физики 9-го класса. Силы сцепления между двумя со- сешпми атомами кремния обусловлены парой валентных электронов, находящихся в основном между атомами. Эта парноэлектронная связь изображается двумя параллельными отрезками, соединяющими кружки (атомы Si). На рисунке 5.4, а все валентные электроны находятся «на своих местах», разорванные связи отсутствуют. Это соответствует полностью заполненной электронами валентной о-зоне.
Если валентному электрону сообщить достаточную энергию, то связь может разорваться. Такой оторвавшийся электрон на зонной схеме соответствует электрону в зоне проводимости. Минимальная энергия, необходимая для разрыва связи, и есть ширина запрещенной зоны гг Место, откуда ушел электрон, остается вакантным. Это дырка в валентной зоне, обладающая избыточным положительным зарядом. На рисунке 5.4, б имеется два свободных электрона и две дырки, что соответствует зонной схеме, изображенной на рисунке 5.3.
Собственная проводимость. До сих пор мы полагали, что проводимость полупроводника возникает потому, что некоторое количество электронов перешло из у-зоны в с-зону. Ток состоит из дырочного и электронного, причем концентрация дырок равна концентрации электронов: п р. Такая проводимость называется собственной проводимостью.
Согласно формуле (7), величина собственной проводимости X определяется четырьмя* величинами: п, /?, |1п и Подвижности рп и \ipв одних случаях возрастают с увеличением температуры, в других убывают. В чистом (не содержащем примесей) полупроводнике концентрации пир всегда растут с повышением температуры (рис. 5.5), причем настолько быстро, что Хп и кр и, следовательно, полная проводимость чистого полупроводника X всегда увеличиваются с повышением температуры.
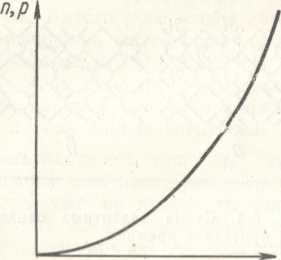
Рис. 5.5. Зависимость концентрации свободных носителей (л, р) в чис¬том полупроводнике от температуры.
