Магнитный момент ферромагнетика можно искусственно заставить вращаться, поместив ферромагнетик во вращающееся магнитное поле. Если частота вращения магнитного поля отличается от собственной частоты вращения магнитного момента, магнитное ноле будет то ускорять магнитный момент, то тормозить («забирать» у него энергию). В среднем магнитный момент вовсе не воспримет энергии вращающегося магнитного поля. И эксперимент, поставленный так, чтобы измерить поглощенную ферромагнетиком энергию переменного магнитного поля, ничего не покажет.
По если частота переменного вращающегося магнитного поля совпадет с собственной частотой вращения магнитного момента, то наступает резонанс и энергия магнитного поля поглощается. Обычно эксперимент ставят так: помещают ферромагнитный образец в резонатор, в котором имеется переменное электромагнитное поле определенной частоты. Весь прибор (резонатор с ферромагнитным' образцом в нем) помещают во внешнее постоянное магнитное поле. Повторяя эксперимент, изменяют величину внешнего постоянного магнитного поля Я, при этом меняется частота вращения магнитного момента (см. формулу 7). При некотором значении Я = Ярез резко возрастает количество поглощаемой в резонаторе энергии Я/7, что и свидетельствует о резонансе (рис. 4.8).
Этот резонанс называют ферромагнитным. Ферромагнитный резонанс был открыт Дж. Гриффитсом (1946 г.).
Порядки величии таковы: магнитному полю Я в 10 ООО гс по формуле gH= со соответствует частота со « 1011 1 [сек или длина волны К ^ 6 мм%.
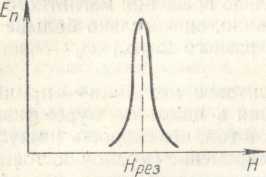
Рис. 4.8. При определенном (резонансном) значении магнитного поля И = /Урез резко возрастает поглоще¬ние электромагнитной энергии ферромагнетиком. Это — ферромагнитный резонанс. Еп поглощенная энергия.
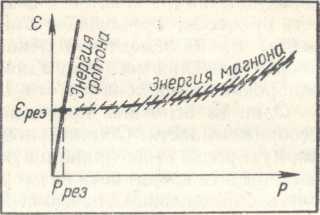
Рис. 4.9. Точка пересечения определяет резонансное значение импульса р и энергии е фотона и магнона. Резонансный импульс очень мал. Размытие показывает, что энергия магнона имеет некоторую неопределенность, обусловленную конечным временем его жизни.
Ферромагнитный резонанс допускает квантовомеханическую трактовку. Как известно, электромагнитную волну определенной частоты при квантовом подходе надо рассматривать как частицу
(фотон), импульс которой равен р = , а энергия равна ftco
с
(со — частота электромагнитной волны). Тогда поглощение электромагнитной энергии ферромагнетиком следует трактовать как превращение фотона в магнон. Превращение, как всякий физический процесс, может произойти, если выполнены законы сохранения энергии и импульса. Их выполнение легко проанализировать по рисунку 4.9, на котором показаны зависимости энергии фотона и магнона от импульса. Зависимость энергии е (р) магнона от импульса р дана формулой (10). Кривые пересекаются при таком значении импульса, когда возможно резонансное превращение фотона в магнон. Надо только учесть, что нам пришлось несколько исказить рисунок. Скорость света так велика, что прямая, изображающая зависимость энергии фотона от импульса, должна практически совпадать с осью ординат. А это значит: при превращении фотона в магнон «рождается» магнон с почти нулевым импульсом. Ферромагнитный резонанс дает возможность непосредственно измерить энергию покоя магнона — «взвесить» покоящийся магнон.
Мы несколько упростили рассказ. Поглощенная ферромагнетиком энергия отлична от нуля не только, когда частота фотона совпадает с частотой однородной прецессии, но и вблизи резонансного значения магнитного поля (рис. 4.8). Причина этого состоит в следующем. Вращение магнитного момента не может продолжаться бесконечно (на квантовом языке: магнон не живет вечно). Всегда есть процессы, приводящие к замедлению вращения магнитного момента. Время замедления т, как правило, значительно больше периода- вращения магнитного момента, равного 2зт/со0; c«v—частота однородной прецессии (щ = е0/Й).
а с
Один из основных принципов квантовой механики — принцип неопределенности. Обычно упоминаемая в школьном курсе физики формулировка этого принципа состоит в том, что скорость (импульс) частицы и ее координата не могут одновременно (в одном состоянии) иметь определенные значения. Из этого делается вывод, что атомные частицы не движутся по определенным траекториям.
Нам здесь следует обратиться к несколько иной форме принципа неопределенности. Частица (любая атомная система) может иметь определенную энергию только, если рассматриваемое состояние живет вечно. Если же речь идет о состоянии, которое живет время т, то энергия этого состояния может быть определена с точностью, не превышающей значение ft/т. В нашем случае это означает, что энергия магнона определена с точностью, не большей Й/т, и на рисунке 4.9 надо изобразить не линию, а полоску шириной Й/т. Неопределенность энергии магнона приводит к возможности превращения «фотон— магнон» в некотором интервале значений магнитного поля. И другой вывод: исследуя кривую поглощения (форму резонансной кривой, рис. 4.8), можно узнать о процессах, ограничивающих время жизни магнона. Это очень интересно, так как позволяет изучить взаимодействие магнона с магнонами и с квазичастицами другой природы.
Ферромагнитный резонанс — метод определения энергии покоя магнона. А можно ли непосредственно исследовать свойства отдельного подвижного магнона (подчеркиваем, что речь идет об изучении отдельного магнона)? Коллектив магнонов доступен экспериментальному изучению (об этом уже говорилось), однако выводы убедительней, сведений больше, если удается «изолировать» объект исследования и иметь дело с одним «подопытным». Природа предоставила нам такие возможности.
Длина волны света очень велика по атомным масштабам. Поэтому при ферромагнитном резонансе возбуждается бесконечно длинная спиновая волна (точнее, такая длинная, что мы можем считать ее бесконечной). А нельзя ли сжать электромагнитную волну, укоротить ее? В оптически плотной среде с показателем преломления п длина волны света в п раз меньше, чем в вакууме. Но показатель преломления я, в лучшем случае, равен нескольким единицам. Поэтому надеяться на значительное сжатие за счет показателя преломления не приходится. Исключение составляют металлы. В металлы электромагнитные полны вообще почти не проникают, а та незначительная часть, которая проникает, затухает на очень малом расстоянии. Это расстояние в диапазоне длин волн, приблизительно равных одному сантиметру, составляет около 10~б см, т, е. электромагнитное поле в металле существенно изменяется на расстояниях, в сто тысяч раз меньших, чем его длина волны в вакууме.
Затухающее электромагнитное поле можно представить в виде суммы (суперпозиции) плоских волн и убедиться, что главный вклад в эту сумму дают волны с длиной, приблизительно равной 10~5 см, в то время как на поверхность металла падает волна длиной « 1 см. Другими словами, металл совершает огромное сжатие электромагнитных волн, правда, несколько «размывая» их: вместо одной плоской волны возникает пакет — совокупность волн, сумма (суперпозиция) которых создает затухающее в глубину металла поле.
Сжатие электромагнитной волны металлом используется для изучения подвижных магнонов. Для этого надо измерить зависимость коэффициента отражения электромагнитной волны поверхностью ферромагнитного металла от частоты и от внешнего постоянного магнитного поля. Конечно, измерения следует проводить в условиях, близких к условию ферромагнитного резонанса.
Естественная возможность исследования спиновых волн конечной длины связана с резонансным возбуждением стоячих спиновых волн в ферромагнитной пластине. Действительно, из-за того что спиновая волна отражается границами пластины, в пластине образуются стоячие спиновые волны. На толщине пластины должно укладываться целое число полуволн. А это означает, что в пластине могут возбуждаться спиновые волны с вполне определенными частотами (их можно найти, если в формулу (9) вместо X подставить 2d/n, где d— толщина пластины, а п — целые числа; напомним, что частота равна энергии магнона, деленной на постоянную Планка й; со = е/Л). Возбуждение стоячих спиновых воли устанавливает связь между частотой спиновой волны и ее длиной, т. е. определяет закон дисперсии спиновых волн.
Исследование высокочастотных свойств пластин (тонких пленок) постепенно становится важным средством изучения динамики магнонов.
Однако с помощью описанных методов нельзя -(или необычайно трудно) исследовать спиновые волны, длина которых порядка межатомных расстояний, или, на корпускулярном языке, магноны с большими импульсами. «Подобраться» к магнонам с большими импульсами помогают всепроникающие нейтроны. Прохождение нейтрона через магнитный кристалл сопровождается своеобразным резонансным эффектом— рождением магнона[1]. Расскажем о нем несколько подробнее. Нейтрон, пролетая через магнитный кристалл, взаимодействует с магнитными моментами атомов (ведь он сам обладает магнитным моментом!) и заставляет их двигаться — вращаться (переворачиваться). Или, другими словами, нейтрон возбуждает спиновые волны. Корпускулярные свойства волны (в данном случае спиновой) проявляются в том, что энергия волны может быть hw, 2/гсо и т.д., а импульс: 2яА/Х, 4л/tikи т. д. (со и Я—частота и длина спиновой волны). «На языке магнонов» это звучит так: рождается один магнон с энергией в = Асо и импульсом р = 2 л АД, два магнона... и т. д. Расчет показывает, что рождение одного магнона значительно более вероятно, чем двух или большего числа.
Акт рождения магнона, как и любой процесс в природе, ; подвластен законам сохранения энергии и импульса, которые в данном случае приобретают такой вид:
р2 — Pi= q, е2 — = ft<o, (12)
где q— единичный вектор в направлении распространения спиновой волны, Асо — энергия магнона, а рг — рх и е2 — ех — изменения импульса и энергии нейтрона. Для определения рг — piи в2— ег достаточно измерить скорость нейтрона, летящего в данном направлении (если известны скорость и направление полета нейтрона до рассеяния, т. е. р1 и еД В этом заключается эксперимент.
Таким образом, измеряя р2— Р\ и е2— ех и используя законы
сохранения энергии и импульса, можно непосредственно измерить закон дисперсии магнонов — зависимость его энергии от импульса. Этот метод получил в последние годы широкое распространение, так как у экспериментаторов, благодаря развитию ядерной техники, появились в распоряжении мощные пучки нейтронов, а развитие электронно-вычислительных машин дало возможность механизировать обработку результатов подобных (очень трудоемких) опытов. Рассеяние нейтронов — основной поставщик сведений о маг- нонах, импульс которых сравнительно велик.
Однородное вращение магнитных моментов, как мы знаем, возможно не только в ферромагнетиках, но и в антиферромагнетиках. Это означает, что резонансное поглощение энергии переменного магнитного поля возможно не только в ферромагнетиках, о которых речь шла в этом разделе, но и в антиферромагнетиках. Особенно убедительно это утверждение звучит, если сформулировать его на квантовом языке: фотон при взаимодействии с антиферромагнети- ком превращается в магнон.
Антиферромагнитиый резонанс впервые наблюдался группой голландских физиков в 1951 г. и после этого стал одним из распространенных методов исследования антиферромагнетиков. Существенное развитие он получил в работах советского академика А. С. Боровика-Романова и его учеников.
Физическая природа антиферромагнитного резонанса, по существу, не отличается от природы ферромагнитного резонанса. Поэтому нет необходимости повторять сказанное в этом разделе. Интересно, однако, подчеркнуть различия, обусловленные антифер- ромагнитным упорядочением магнитных моментов.
Во-первых, спектр антиферромагнетика сложнее, чем спектр ферромагнетика. Во-вторых, у большинства антиферромагнетиков энергия покоящегося магнона значительно больше энергии покоящегося магнона ферромагнетика (частота сол очень большая, см. формулу 11). Для антиферромагнетиков резонанс находится в недоступной или труднодоступной области частот, поэтому надо использовать огромные магнитные поля, так как, согласно формуле (11), одна из частот неоднородного вращения уменьшается с ростом внешнего магнитного поля.
