Что это за энергия е₀? На что она расходуется? На отклонение маг­нитного момента от наиболее энергетически «выгодного» направле-

ния, т. е. направления, совпадающего с вектором напряженности магнитного поля.

Магнитное поле удерживает магнитный момент в определеннохМ направлении (поэтому г₀ Ф 0). Но это внешняя по отношению к телу сила. А нет ли внутренних сил, играющих похожую роль? На­помним, что обменные силы (главная причина возникновения спон­танной намагниченности) для этого не пригодны, ибо для них без­различно, куда направлен магнитный момент (см. выше). Силы, реагирующие на направление магнитного момента в ферромагнети­ках (и в антиферромагнетиках), есть. Их так и называют— анизо­тропными силами (чаще говорят об энергии анизотропии). Суще­ствование энергии анизотропии проявляется в том, что е₀ больше, чем 2рЯ, а значит, и частота прецессии со больше gH. Мы ее по- прежнему будем обозначать со, а энергию — е₀.

Природу энергии анизотропии разъяснить непросто, так как во всех подробностях она не ясна до сих пор. Но главное понято. Магнитные моменты атомов, обусловленные спинами, взаимодей­ствуют с их орбитальными моментами, а последние определяются пространственным движением электронов, которое существенно зависит от взаимного расположения атомов в кристаллической ре­шетке. В результате энергия магнитных моментов (спинов) "зави­сит не только от их взаимной ориентации, но и от поворота магнит­ной системы относительно осей кристалла.

Интересно отметить, что величина энергии анизотропии суще­ственно зависит от симметрии кристалла. У кубических кристал­лов она меньше, а у гексагональных больше.

Разобьем ферромагнетик на небольшие объемы. Каждый из них обладает местным (локальным) магнитным моментом. Вращение маг­нитного момента тела можно представить себе как софазное (син­хронное) вращение всех локальных магнитных моментов. В каждый момент времени все магнитные моменты параллельны друг другу. Но когда магнитные моменты не изменяют взаимного расположения, то обменные силы не действуют. Поэтому-то частота однородной прецессии и величина е₀ не зависят от обменных сил.

Рассмотрим теперь более сложное (волнообразное) движение локальных магнитных моментов. Ясно, что энергия такого движе­ния должна складываться из двух частей: энергии, требуемой на отклонение магнитного момента от оси, е₀ и энергии волны под действием обменных сил. Если длина волны велика, то, согласно формуле (4):

Существование энергии анизотропии или внешнего магнитного поля приводит к тому, что частота спиновой волны даже при бес­конечной длине волны (к = ос) отлична от нуля, или, на квантовом языке: магнон с импульсом, равном нулю, имеет отличную от нуля энергию. Его энергия покоя равна е₀. У обычных частиц энер­гия покоя равна тс²> где т — масса частицы, а с— скорость света. Можно вычислить массу покоя магнона т₀ — е₀/с². Эта величина баснословно мала: при Н — 10 ООО гс (\хН при этом чаще всего боль­ше энергии анизотропии) т₀ ж 10~⁸⁷ г, т. е. в 1Q¹⁰ раз меньше массы самой легкой частицы— электрона.

И все же эксперименты, исследующие высокочастотные свой­ства ферромагнетиков (но о них позже, в следующем разделе), тепловые и магнитные свойства при очень низких температурах, дают возможность обнаружить энергию покоя магнона.

Мы уже сравнивали рЯ и кТ и установили, что при Т = ГК равенство достигается, если Я = Ю⁴ гс. Если охлаждать ферромаг­нетик и дальше, то тепловой энергии может не хватить на рождение магнонов. При сверхнизких температурах магнонов очень мало. Закон 3/2 оказывается справедливым не до абсолютного нуля. Тем­пературная зависимость магнитного момента и теплоемкости при очень низких температурах содержит энергию покоя м .гнона, что и дает возможность «взвесить» частицу, масса которой в 10¹⁰ раз меньше массы электрона!

Теперь об антиферромагнетиках. Для описания их магнитных свойств каждый элемент объема надо наделить двумя магнитными моментами, которые в основном состоянии и когда к антиферромаг­нетику не приложено магнитное поле (Я = 0), строго аитипарал- лельны, а по величине равны друг другу. Их вращение в виде волн может распространяться по кристаллу. Поскольку моментов два, то и волны две, при Я 0 их частоты равны. Когда напряженность внешнего магнитного поля отлична от нуля, то частоты различны:

^Ю1 —     + gtti                                     (11)

*>2 = 0) _A-gH.

Здесь со_А — частота прецессии магнитных моментов аитиферро- магиетика в отсутствие внешнего магнитного поля. Частота со_л в антиферромагнетике, как правило, больше соответствующей часто­ты в ферромагнетике. Ведь при отклонении от оси магнитные мо­менты действуют не только против сил анизотропии, но и против обменных сил. Внешнее магнитное поле увеличивает одну частоту и уменьшает другую. Для одного из магнитных моментов оно — союзник энергии анизотропии, для другого— противник.

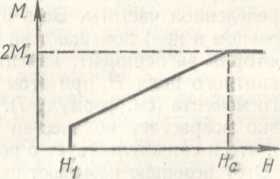
Формулы (11) справедливы в не слишком больших магнитных полях. Е1а рисунке 4.5 показано, как изменяется расположение магнитных моментов под действием приложенного магнитного поля. Частоты вращения «чувствуют» положение магнитных моментов При определенном значении напряженности магнитного поля (gH1 = со_л) магнитная структура изменяется, так как энергетиче­ски выгодно расположение магнитных моментов почти перпендику­лярно оси анизотропии (рис. 4.5, б). При дальнейшем увеличении магнитного поля угол между магнитными моментами уменьшается, и, наконец, при некотором значении напряженности магнитного поля (Я = Я_с) оба магнитных момента устанавливаются парал­лельно gch анизотропии (рис. 4.5, в) — магнитные м менты «схлопы- ваются». Правда, величина поля «схлопывания» Я_с очень велика, энер­гия рЯ_с при этом приблизительно равна обменной энергии k&_M. Перестройка магнитной структуры отчетливо проявляется в зави­симости магнитного момента антиферромагнетика от магнитного поля (рис. 4.6).

Из-за сравнительно большой величины энергия покоя магнона при Я = 0 велика. Темпера­турная зависимость термодина­мических величшг антиферрома- гнетиков позволяет измерить энергию покоя магнонов в ан­тиферромагнетиках, производя эксперименты при более высоких температурах, чем нужны для аналогичных целей в экспери­ментах с ферромагнетиками.

Правда, это относится только к тем антиферромагнетикам, магнитным моментам которых энергетически выгодно распо­лагаться вдоль оси анизотропии.

Но есть и другие (их даже боль­ше, чем тех, о которых было рас­сказано выше). В них магнитные моменты располагаются в плос­кости, перпендикулярной оси анизотропии (рис. 4.7). Как ори­ентированы магнитные моменты в плоскости — безразлично. По­этому одна из частот однород­ного вращения равна нулю, а другая — примерно такая же, как и у тех антиферромагнети­ков, у которых магнитные мо­менты параллельны оси анизо­тропии.

Описаны только частоты од­нородных колебаний и энергии покоя магнонов. Неоднородным колебаниям (с конечной длиной волны) соответствуют движущиеся магноны, но о них достаточно подробно было рассказано в пре­дыдущем разделе.

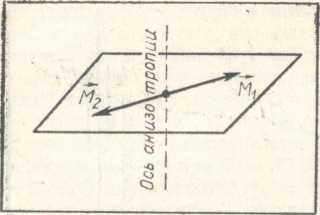
Рис. 4.7. При определенном знаке энергии анизотропии магнитным мо¬ментам выгодно располагаться в плоскости, перпендикулярно оси анизотропии.