Сверхтекучий гелий II — это жидкость, существующая лишь при достаточно низких температурах. Поэтому для объяснения его свойств нам необходимо сначала установить общие закономерности, связанные с изменением характера теплового движения в любом веществе при понижении температуры. Для выяснения этих закономерностей проследим за изменением характера теплового движения в широком температурном интервале начиная с температур, значительно превосходящих комнатную.
При комнатных температурах существуют твердые тела, жидкости и газы. Если начать повышать температуру, то все твердые тела и жидкости превращаются в газ, т. е. в систему, состоящую из отдельных свободно движущихся молекул. При дальнейшем повышении температуры тепловое движение атомов, входящих в состав молекул, становится столь интенсивным, что молекулы начинают распадаться на отдельные атомы. При еще более высоких температурах (фактически это температуры порядка десятков тысяч градусов) то же самое происходит с атомами, они распадаются на электроны и атомные ядра. При столь высоких температурах любое вещество, таким образом, представляет собой газ, состоящий из свободных электронов и ядер.
Элементарные возбуждения. Вернемся теперь к нашей задаче и проследим за процессом понижения температуры, начав с темпера-туры порядка десяти тысяч градусов. Что произошло, когда электроны и ядро объединялись в атом? Для нас существенно следующее. До объединения каждый электрон и ядро имели возможность независимо двигаться в пространстве. После объединения возможно свободное движение лишь всего атома в целом. Электроны и ядро могут двигаться теперь только вместе. Можно сказать, что с понижением температуры уменьшилось число возможных видов теплового движения.
При дальнейшем понижении температуры все новые и новые виды теплового движения исчезают или, как говорят, вымерзают. Вслед за движением электронов относительно ядра вымерзает дви-жение атомов относительно центра тяжести молекулы. При комнатных и более низких температурах можно вообще забыть о том, что молекулы состоят из атомов, которые в свою очередь состоят из электронов и ядра, и считать, что тепловое движение есть движение молекул, рассматриваемых как неделимые частицы. Когда газ или жидкость затвердевают, молекулы уже не имеют возможности перемещаться в пространстве на сколько-нибудь заметные рассотяния, а совершают лишь малые колебания вблизи положений равновесия.
Процесс вымерзания видов движения происходит, конечно, и при температурах ниже комнатных. Так как при абсолютном нуле вообще все виды теплового движения должны исчезнуть, то ясно, что при достаточно низких температурах во всяком веществе эффективен лишь какой-то один, наиболее устойчивый к вымерзанию вид теплового движения. Эот вид движения называют элементарными возбуждениями. Элементарные возбуждения в разных веществах различны. Поэтому основная задача, возникающая при иследовании свойств какого-либо вещества при очень низких температурах заключается в выяснении природы его элементарных возбуждений.
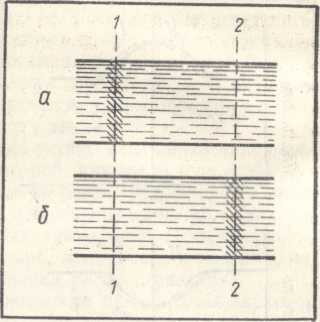
Начнем с движения области уплотнения. Распределение плот-ности жидкости в пространстве в некоторый момент времени можно изобразить в виде графика (рис. 1.6, а), где показана зависимость плотности от координаты х, отсчитываемой вдоль направления движения. С течением времени область повышенной плотности изменяет свое положение. Можно считать, что кривая на рисунке 1.6, а перемещается с такой же скоростью вправо относительно координатных осей. Через малый промежуток времени кривая сместится вправо на малое расстояние и займет положение, показанное на рисунке 1.6, а пунктиром.
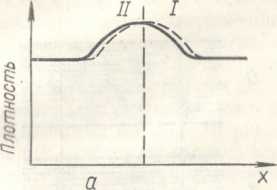
Однако следует подчеркнуть, что скорость самой жидкости в волне мала, значительно меньше скорости звука. Обычно изменение плотности в звуковых волнах мало по сравнению с самой плотностью, т. е. мала неоднородность плотности. Поэтому и скорость жидкости, возникающая из-за этой неоднородности, будет малой. Жидкость в волне двигается, таким образом, значительно медленнее самой волны, и именно поэтому можно говорить о движении уплотнений как о движении волн в практически неподвижной жидкости.
Полученный результат показывает, что область уплотнения всегда находится в движущейся (хотя и медленно) жидкости, т. е. уплотнение распространяется в действительности не в покоящейся жидкости, а в жидкости, движущейся в том же направлении. Поэтому скорость уплотнения есть сумма скорости звука (т. е. скорости относительно неподвижной жидкости) и скорости самой жидкости. Область уплотнения распространяется, следовательно, со скоростью, несколько превышающей скорость звука. Она как бы сама себя ускоряет, порождает такое движение жидкости, которое способствует увеличению скорости распространения.
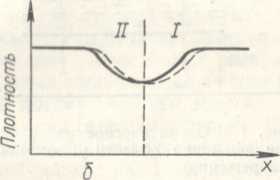
В случае области разрежения результат будет обратным. Действительно, перемещение области пониженной плотности вправо (из положения, соответствующего сплошной кривой на рисунке 1.6 б, в положение, соответствующее пунктирной кривой) приводит, как видно из рисунка, к понижению плотности в области I и к её повышению в области II. Поэтому жидкость должна перетекать из области I в область II, т. е. двигаться в направлении, противо-положном направлению распространения. Скорость перемещения разрежения равна при этом разности скорости звука и скорости жидкости. Область разрежения двигается, таким образом, со ско-ростью, несколько меньшей скорости звука.
Сказанное дает возможность легко установить направление пере-носа массы звуковой волной, в которой, как мы видели, избыточная масса областей уплотнения всегда равна «недостающей» массе областей разрежения. Поскольку уплотнения двигаются быстрее, именно они определяют направление суммарного переноса массы. Распространение звука, следовательно, всегда сопровождается пе-реносом массы жидкости в направлении распространения.
Можно сказать так. Частицы жидкости при наличии звуковой волны совершают колебательное движение. Они двигаются то в направлении распространения волны, то в противоположном направлении аналогично тому, как двигается предмет на поверхности моря под действием волн. Но, если проследить за движением плавающего предмета более внимательно, то будет заметно, что он постепенно сносится в направлении распространения волн. Точно так же постепенно сносятся звуковой волной частицы жидкости. На их колебательные движения накладывается медленное поступательное движение в направлении распространения волны. Но это и значит, что распространение звука сопровождается переносом массы.
Наличие переноса массы в любой системе частиц означает, что
Система обладает отличным от нуля импульсом (количеством движения). Полученный результат показывает, следовательно, что любая звуковая волна обладает импульсом, направленным в направлении распространения волны. С этим фактом связан целый ряд наблюдаемых на опыте явлений. Например, если какой-либо источник то звука излучает направленную волну, то он сообщает ей импульс, а сам испытывает действие силы реакции, направленной в противоположную сторону. Если звук падает на стенку и поглощается ею или отражается, то импульс передается стенке и возникает так называемое звуковое давление.
В жидком гелии II тепловое движение обусловлено наличием звуковых волн. Энергия волн, распространяющихся в различных Направлениях, одинакова, и потому результирующий перенос массы отсутствует. Полученный выше результат показывает, что если по какой-либо причине звуковые волны приобретут преимущественное направление распространенияя, то в этом направлении возникнет перенос массы жидкости.
Излучение звука. Выясним, в каких условиях равномерно движущиеся в жидкости тело может излучать звук. Если на теле установлен, например, источник звука, то излучение будет происходить всегда, при любой скорости тела . Но если равномерно движущееся тело не совершает никаких пульсирующих движений (изменений формы, размеров й т. д.), то (как мы сейчас докажем) излучение звука возможно только при достаточно большой скорости движения.
Состояние жидкости при наличии тела, движущегося с постоянной скоростью, обладает следующим свойством. Представим себе, что мы наблюдаем за процессом, двигаясь вместе с телом. В этой НОВОЙ, как говорят, системе отсчета происходит обтекание жидкостью неподвижного тела. Проследим за движением какой-либо частицы жидкости. Приближаясь с потоком к телу, частица отклоняется от направления своего первоначального движения, изменяет свою скорость и плотность. Пусть теперь в другой момент времени какая-то новая, но такая же частица жидкости начинает двигаться по той же траектории, что и первая. Поскольку с телом с течением времени не происходит никаких изменений, вторая частица двигается в таких же условиях, а потому проделает всю траекторию точно так же, как и первая. А это значит, что в одних и тех же точках траектории параметры частиц (скорость, плотность) одинаковы. Другими словами, плотность и скорость жидкости в любой точке пространства не зависят от времени, т. е. вся картина обтекания не изменяется стечением времени. В нашей первоначальной системе отсчета такая картина должна перемещаться как целое без изменении вместе с телом. Отсюда, в частности, следует, что любые излучаемые телом волны (если таковые имеются) не должны с течением времени изменять своего положения относительно тела.
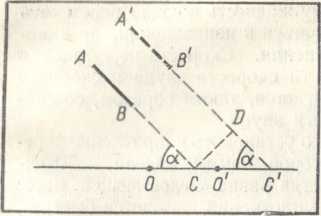
Пусть прямая АВ на рисунке 1.7 представляет собой участок фронта какой-либо волны в данный момент времени, а тело в тот же момент времени находится в точке О. Пусть, далее, тело переместилось со скоростью v в точку О'. За это же время волна, распространяясь в направлении, перпендикулярном фронту, со скоростью звука с переместится из А В в А' В'. Чтобы расположение волны относительно тела не изменялось, расстояние СС' между точками пересечения продолжений двух фронтов с траекторией движения тела должно быть равно пройденному телом пути 00' за время t. Расстояние CD между прямыми АВ и А'В' есть путь, пройденный звуком, за то же время. Из этого следует, что отношение CD к СС' равно отношению скорости звука с к скорости тела u.
Но, с другой стороны, это же отношение равно синусу угла а между фронтом волны и траекторией движения тела, т. е.
Таким образом,
sina=c—. (1)
V
Формула (1) определяет угол, под которым могут быть расположены излучаемые телом волны. Но, поскольку синус любого угла меньше единицы, этот угол действительно существует лишь в случае, когда в правой части формулы (1) стоит величина, меньшая единицы, т. е. когда скорость тела больше скорости звука (v > с).
Тело, движущееся равномерно с дозвуковой скоростью, само по себе звук излучить, следовательно, не может. Тот же результат можно сформулировать и так: излучение звука при дозвуковом обтекании жидкостью покоящегося тела невозможно, поскольку (как мы уже отмечали) задачи об обтекании и движении тела сводится друг к другу простым изменением системы отсчета.
Наглядным проявлением рассмотренного эффекта является из-менение характера излучения звука самолетом, преодолевающим звуковой барьер. Самолет, летящий с дозвуковой скоростью, излучает звук лишь благодаря вибрациям, связанным, в основном, с работой двигателей. При скорости, большей звуковой, интенсивность излучения резко возрастает, поскольку включается механизм непосредственного излучения звука самим самолетом.
Необходимо сделать одну оговорку. При достаточно большой скорости обтекания в жидкости вблизи тела возникает турбулентность, т. е. область нерегулярного вихревого, пульсирующего движения. Эти пульсации так же, как пульсации самого тела или установленного на нем источника звука, могут излучать звук всегда. Фактически турбулентное движение возникает при скоростях, меньших скорости звука, и из-за этого возможно его излучение при дозвуковых скоростях. Для нас важно, что турбулентное движение отсутствует при достаточно малой скорости обтекания, меньшей некоторого критического значения.
Таким образом, можно утверждать, что при обтекании жидкостью любого неподвижного тела со скоростью, меньшей некоторой критической скорости, излучение звука невозможно.
