Гелий не случайно называют инертным газом. Его атомы чрезвычайно слабо взаимодействуют с другими атомами и особенно между собой. Этим объясняется, что гелий переходит из газообразногосостояния в жидкое при рекордно низкой температуре (4,2° по шкале Кельвина) и при дальнейшем понижении температуры не затвердевает вплоть до абсолютного нуля. Твердый гелий существует лишь при повышенном давлении (свыше 25 am), когда из-за уменьшения расстояния между атомами сила взаимодействия возрастает.
В интервале температур от 4,2 до 2,2°К жидкий гелий ведет себя во всех отношениях как обычные жидкости, отличаясь от них лишь величиной некоторых параметров, так, например, плотность его примерно в 7 раз меньше плотности воды. При температуре 2,2°К происходит переход этой обычной жидкости, так называемого гелия I, в особое состояние (гелий II), обладающее свойством сверхтекучеести. Ниже мы рассмотрим несколько наиболее важных экспериментов, проведенных с гелием II, и покажем, что результаты этих экспериментов находятся в разительном противоречии с обычными представлениями о жидкости и для их объяснения необходимо привлечение каких-то новых представлений.
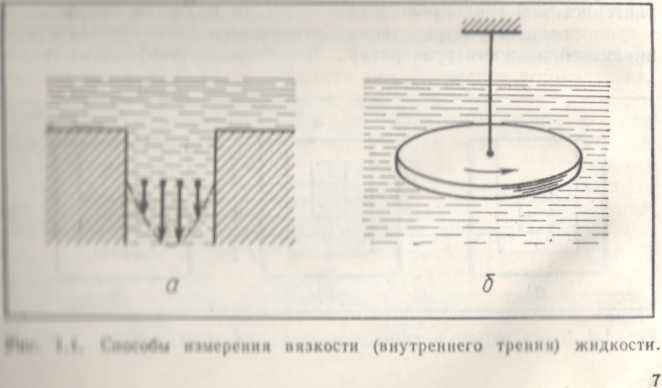
Вязкость и сверхтекучесть. Первая загадка гелия II возникает при измерениях вязкости. В обычных жидкостях вязкость (или, другими словами, внутреннее трение) может быть измерена двумя простейшими способами, дающими, конечно, один и тот же результат. Первый способ заключается в измерении скорости вытекания жидкости из сосуда через узкую щель под действием силы тяжести (рис. 1.1, а). Скорость жидкости, изображенная на рисунке стрелками, максимальна в средней части щели и убывает при приближении к стенке. Различные слои движутся, таким образом, с разными скоростями, и поэтому между ними возникает сила трения, от величины которой зависит скорость вытекания. Второй способ (рис. 1.1, б) заключается в измерении времени затухания крутильных колебаний диска, погруженного в жидкость. Здесь все аналогично первому случаю. Жидкость вблизи диска увлекается его движением, а вдали практически покоится. Различные слои двигаются с разными скоростями, и возникающая сила внутреннего трения приводит в конце концов к тому, что энергия колебаний превращается в тепло. Зная время затухания, можно определить вязкость.
Эксперименты с жидким гелием, проведенные первым способом, показалии, что вязкость гелия I вполне заметна и измерима, но при переходе в область гелия II она скачком падает до неизмеримо малой величины. Из этого эксперимента следует, что вязкость гелия II скорее всего равна нулю или, по крайней мере, во много тысяч раз меньше вязкости гелия I. В последнем случае гелий II можно было бы считать жидкостью, подчиняющейся обычным законам, но обладающей чрезвычайно малой вязкостью. Однако измерения вязкости гелия II вторым способам дают иные результаты. Величина вязкости гелия II в этом случае получается даже больше, чем вязкость гелия I. Таким образом, оказывается, что гелий II, в отличии обычных жидкостей, в одних условиях не обнаруживает вязкости, а в других - его вязкость вполне заметна.
Фундаментальное свойство гелия II—протекать через узкие щели, не обнаруживая вязкости, — названо сверхтекучестью. Сверхтекучесть гелия II весьма эффектно проявляется в опыте, изображенном на рисунке 1.2. Пусть в начальном состоянии (рис. 1.2, а) жидкость частично заполняет два открытых только сверху сосуда (внутренний и внешний), причем так, что уровень жидкости в обоих сосудах одинаков. Поднимем внутренний сосуд относительно внешнего так, чтобы он занял положение, изображенное на рисунке 1.2, б, в, Если производить этот опыт с обычной жидкостью, то возникшая картина будет соответствовать рисунку 1.2, б. Уровень жидкости во внутреннем сосуде станет выше уровня во внешнем как раз на столько, на сколько приподняли внутренний сосуд. Это состояние сохраняется в течение весьма длительного времени. Гелий II ведет себя совершенно иначе. В опыте с гелием II после поднятия внутреннего сосуда будет наблюдаться картина, изображенная на рисунке 1.2, в: уровни жидкости в обоих сосудах по-прежнему одинаковы. Изменяя положение одного сосуда относительно другого, мы не сможем сделать различными уровни жидкости. Гелий II каким-то необычным образом перетекает из одного сосуда в другой и весьма быстро выравнивает уровни.
Перенос тепла и движение. В обычных жидкостях существует два механизма переноса тепла — теплопроводность и конвекция.
Теплопроводность — это передача тепла от более нагретых мест к менее нагретым в неподвижной жидкости. Рассмотрим следующий опыт (рис. 1.3). Нагреватель Н излучает тепло. Если перенос тепла осуществляется посредством теплопроводности, то жидкость неподвижна, а ее температура убывает в направлении, указанном на рисунке стрелкой (слева направо), так что при передаче тепла от болеенагретых мест к менее нагретым возникает поток тепла в этом же направлении. Таким образом, для переноса тепла этим способом необходимо, чтобы термометр Тх показывал более высокую температуру, чем термометр Т2. Количественной характеристикой теплопроводности жидкости является коэффициент теплопроводности, определяемый отношением потока тепла к возникающей разности температур. Чем больше коэффициент тепло-проводимости, тем больший поток тепла переносится в жидкости при той же разности температур или, другими словами, тем меньшая разность температур необходима, чтобы обеспечить один и тот же поток тепла.
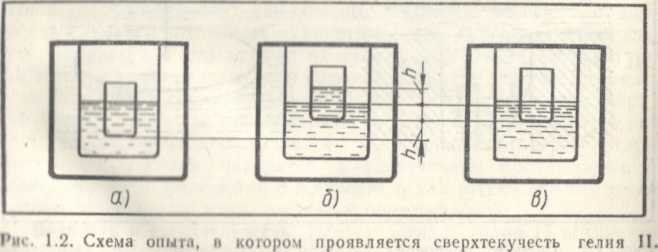
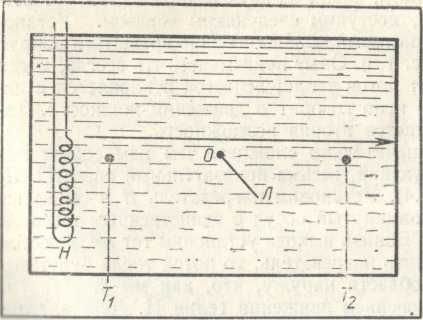
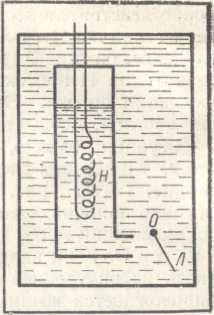
Рис. 1.4. Схема опыта, демонстрирующего перенос тепла в гелии II
Для того чтобы выяснить, какая из двух возможностей соответствует действительности, поступим следующим образом. Установим в гелии лепесток Л, который может свободно вращаться вокруг неподвижной оси О (рис. 1.3). Опыт показывает, что всегда, когда через гелий II протекает поток тепла, лепесток отклоняется в направлении потока. Это ясно говорит о движении жидкости. Таким образом, осуществляется вторая возможность.
Ситуация, однако, значительно сложнее, чем нам сейчас кажется. Проделаем следующий, весьма показательный опыт (П. Л. Капица, 1941 г., рис. 1.4). Установим нагреватель Н в гелии II, частично заполняющем замкнутый сосуд с единственным выходом в окружающий гелий II. Вблизи выхода установим тот же лепесток Л на оси О. Если включить нагреватель, то поток тепла будет вытекать из внутренней области наружу, что, как мы уже знаем, сопровождается возникновением движения гелия II. Действительно, лепесток Л отклоняется вправо, показывая, что жидкость вытекает из сосуда. Но теперь мы с удивлением обнаружим, что уровень жидкости в сосуде не понижается. Можно производить опыт как угодно долго. Лепесток все время будет отклонен, так что жидкость, казалось бы, непрерывно вытекает, однако уровень остается на месте. С учетом закона сохранения массы последний результат убедительно показывает, что законы движения гелия II должны принципиально отличаться от обычных законов движения жидкости.
